К ВОПРОСУ ОПРЕДЕЛЕНИЯ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ГИДРОТЕХНИЧЕСКИХ СООРУЖЕНИЙ ПРИ ВЗРЫВАХ
Манукян Л. А. (ИГИС НАН РА)
Важной характеристикой, описывающей динамические свойства сооружения, является функция частотной характеристики (ЧХ). Теоретическое определение ЧХ сложных сооружений, например гидротехнических, связано с большими и практически непреодолимыми трудностями аналитического и вычислительного характера.
В работе рассматриваются вопросы экспериментального оценивания ЧХ гидротехнических сооружений при взрывных воздействиях. Приводятся результаты определения ЧХ земляной плотины Гегардаличского водохранилища.
1.Постановка задачи и метод решения.
Рассмотрим стационарную линейную систему с весовой функцией h(t), t,
[t0,
∞).
Предполагается, что система физически реализуема и h(t) абсолютно
интегрируема на (-
∞,∞).
Пусть {x(t),
t[t0,t1]},
{y(t),t
[t0,t1]}
входной и выходной переходные случайные процессы с нулевыми математическими
ожиданиями M[x(t)]=0, M[y(t)]=0.Предполагается, что выход содержит
посторонний шум, например, зависящий от сигнала инструментальный шум. К
нестационарным случайным процессам, которые существуют физически лишь на
протяжении конечных и измеримых интервалов времени относятся, например,
взрывные воздействия. Переходные процессы допускают использование
существенно более простых методов анализа, основанных на финитном
преобразовании Фурье. Оптимальная ЧХ H(f) системы, которая минимизирует шум
на выходе, удовлетворяет следующему соотношению [1]
Pxy(f)=H(f)Pxx(f), f (-∞,
∞),
(1)
где P xx(f)=M[X *(f)X(f)] - функция спектральной плотности энергии (СПЭ) входного процесса {x(t)}, Рxy(f)=М[Х* (f)Y(f)] – функция взаимной СПЭ между входным {x(t)} и выходным {y(t)} процессами, X(f), Y(f) — финитные преобразования Фурье входного x(t) и выходного y(t) — сигналов, Х *(f) — комплексное сопряжение X(f), f- частота. Система оптимальна в том смысле, что ЧХ H(f) удовлетворяющая соотношению (1), является функцией, которая формально задает наилучшую в среднеквадратическом смысле линейную связь между процессами {x(t)} и {y(t)}.
Теоретически в случае переходных процессов операция усреднения, необходимая для получения оценок СПЭ, подразумевает, что эксперимент, в результате которого получены реализации процессов, может быть повторен многократно. На практике, часто по техническим или экономическим соображениям, удается осуществить лишь несколько экспериментов. В таких случаях для получения статистически состоятельных оценок СПЭ целесообразно применять специальные методы спектрального оценивания. Воспользуемся периодограммным методом Уэлча. Метод Уэлча основан на создании псевдоансамбля периодограмм за счет деления последовательности на N перекрывающихся сегментов. Перед вычислением периодограммы каждого сегмента этот сегмент обрабатывается с помощью временного окна. Среднее значение периодограмм взвешенных сегментов дает оценку периодограммы Уэлча [2]
w(f)=
w(n)(f),
где
w(n)-
выборочный СПЭ взвешенного
n-го сегмента. Дисперсия периодограммы Уэлча
примерно обратно пропорциональна числу сегментов D[w(f)]
∞ Рw2(f)/N,
а спектральное разрешение не превосходит величину, обратной длине сегмента.
Оценку ЧХ определяем из следующего выражения
xy(f)/
xx(f)
гдеxx(f),
xy(f)-оценки
СПЭ, вычисленные периодограммным методом Уэлча.
2.Инженерный расчет. Приведем некоторые результаты вычислений ЧХ земляной плотины Гегардаличского водохранилиша. Общая протяженность плотины составляет 550м при максимальной высоте 15м. По верхнему бьефу плотины были установлены три инженерно-сейсмометрических профиля. В каждый профиль входили три точки наблюдений.
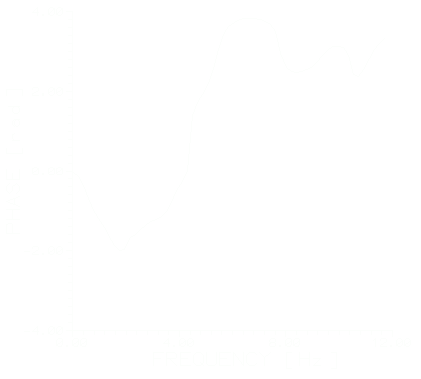
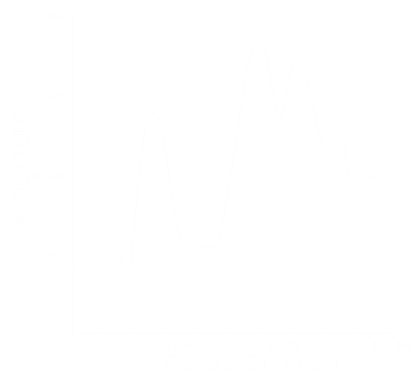
Рис.1. Инструментальные записи скоростей в ИТ1 и ИТ3 при первом взрыве.
Измерительные точки условно обозначены следующим образом ИТ1- основные (h=0м) ИТ2- промежуточная точка (h=9м), ИТ3-гребень (h=15м), где h- относительная высота точки наблюдения. Колебания плотины возбуждались с помощью взрывов. Во всех измерительных точках зарегистрировались скорости колебания плотины в поперечном направлении. Точка ИТ1 принимается входной,ИТ2, ИТ3-выходные точки, H1j(f), j=2,3 ЧХ плотины. Отметим, что при проведении экспериментальных работ уровень воды в водохранилище находилась на нулевой отметке. Дальнейшее изложение результатов относится к среднему профилю. Реализации скоростей зарегистрированные в измерительных точках ИТ1 и ИТ3 при первом взрыве показаны на рис. 1. На рис. 2 и 3 показаны оценки амплитудного спектра ЧХ H13(f) при первом и втором взрывах.
Графики, приведенные на рис. 2, соответствуют выборочным оценкам.
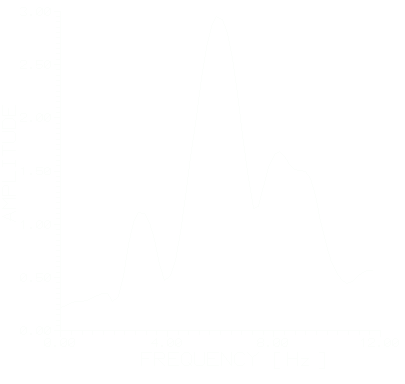
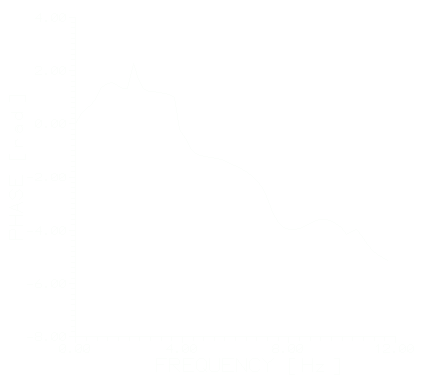
Рис.2. Выборочные оценки Рис.3. Периодограммные оценки
амплитудного спектра H13(f) амплитудного спектра H13(f).
1-I взрыв, 2-II взрыв. 1-I взрыв, 2-II взрыв.
Оценки, вычисленные периодограммным методом Уэлча,показаны на рис.З. В принципе, исходя из физического смысла решаемой задачи, оценки приведенные на рис. 2 должны быть идентичными, т. к. ЧХ линейной системы не зависит от вида входного воздействия.
Рис.4. Усредненная оценка H12(f) по результатам двух взрывов.
Сравнивая эти оценки, видим, что они сильно флюктуируют и существенно отличаются между собою. Следовательно, выборочные оценки ЧХ статистически несостоятельны. Применение метода Уэлча позволяет уменьшить дисперсию и получить устойчивые результаты. Сравнивая графики, приведенные на рис. 3 видим, что оценки модуля ЧХ определенные этим методом почти идентичны. На рис. 4 и 5 приведены периодограммные оценки ЧХ (амплитуда и фаза) Н12(f) и Н13(f), усредненные по результатам двух экспериментов.
Рис.5. Усредненная оценка H13(f) по результатам двух взрывов
Амплитудные спектры, представленные на рис. 4 и 5, выделают две резонансные f1=3 Гц — основная гармоника колебаний плотины, f2=6 Гц— вторая гармоника. Интересной особенностью полученных результатов является тот факт ,что в амплитудном спектре Н12(f) (рис. 4) почти отсутствует второй тон колебаний Приближенное значение коэффициента демпфирована соответствующее основному тону колебаний плотины ξ1=0.2, определен методом измерения ширины полосы резонанса [3].
ЛИТЕРАТУРА
1. Бендат Дж. Основы теории случайных шумов и ее применения. М.: Наука,1965. 464с.
2. Рабинер П., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир, 1978. 848с.
3. Нашиф А., Джоунс Д., Хендерсон Дж. Демпфирование колебаний . М.: Мир, 1988. 448с.
