МОДЕЛИРОВАНИЕ УСКОРЕНИЙ СИЛЬНЫХ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЙ НА ОСНОВЕ ЗАПИСЕЙ СЛАБЫХ ЗЕМЛЕТРЯСЕНИЙ

МАНУКЯН Л. А.(ИГИС НАН РА)

На основе инструментальных записей ускорений слабых землетрясениях с магнитудой 3≤M≤5 с помощью вычисленной функции преобразования, моделируются акселерограммы сильных землетрясений, которые в целом отражают основные региональные особенности сотрясаемой площадки. Приводятся примеры моделированных акселерограмм для двух регионов Армении: Ванадзор и Гюмри.

1.Постановка задачи. Инструментальная запись землетрясения (сильного или слабого) содержит в себе информацию о механизме очага, геологических особенностях на трассе распространения сейсмических волн, количестве освобожденной энергии, локальных грунтовых условиях на участке регистрации и т. д. При использовании записей слабых землетрясений для моделирования искусственных акселерограмм, перечисленные параметры учитываются автоматически. Принципиальное количественное различие между записями слабых и сильных землетрясений (при равных гипоцентральных расстояниях, идентичных геологических условиях среды распространения сейсмических волн и т. д.) состоит в том, что они различаются амплитудным уровнем во временной и соответственно, в частотной областях. Таким образом, проблема заключается в нахождении (определении) зависимости преобразования временной или частотной характеристики слабого землетрясения в соответствующую характеристику сильного землетрясения. Более подходящей для этой цели является частотная характеристика. Воспользуемся следующей эмпирической зависимостью [1,2]:

lgFS(T)=M+A+b₁(T)M+b₂(T)h+b₃(T)v+b₄(T)+b₅(T)M² (1)

где Т – период колебания, FS(T) – амплитудная функция спектра Фурье, М – магнитуда землетрясения, h – толщина осадочных пород, v – коэффициент, принимающий значение 0, если вычисляется спектр горизонтального составляющего колебания грунта, и значение 1 для спектра вертикального составляющего, b_i (T), i=1,...,5 – коэффициенты, определенные с помощью регрессионного анализа, A = A (R,H,S,M,T) – функция рассеяния, R – эпицентральное расстояние, Н – глубина гипоцентра, S=S(M,T) – размер очага землетрясения.

Используя (1), определим функцию преобразования спектра землетрясения с магнитудой М₁ в спектр землетрясения с магнитудой М₂. Пусть при этом Т₁= T₂= T, R₁= R₂= R, H₁=H₂=H. Подставляя М₁ и М₂ в (1), составляя разность lgFS₂(T) и lgFS₁(T) получаем следующую функцию преобразования

lgП(M₁,M₂,T)=(M₂-M₁)(1+b₁(T))+b₅(T)(M₂²-M₁²)+A(S₂,M₂,T)-A(S₁,M₁,T) (2)

Формула (2) является основой искусственных акселерограмм. Вид функции преобразования П(М₁,М₂,Т) спектра ускорения землетрясения с магнитудой М₁=3.6 в спектр ускорения землетрясения со значением магнитуды M₂ = 5, 6, 6.9 показан на рис. 1.

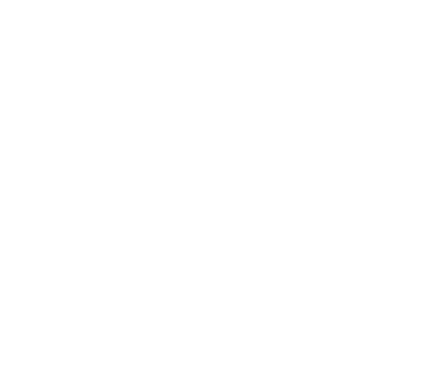
Рис.1. Функция преобразования спектра ускорения исходного землетрясения магнитудой М₁=3.6 в спектр ускорения магнитудой 1. M₂ =5; 2. M₂ =6; 3. M₂ =6.9.

Предположим, что в некоторой заданной площадке получена инструментальная запись слабого землетрясения с параметрами φ ,λ, R, H, M₁, тогда используя формул (2), можно преобразовать спектр ускорения слабого землетрясения FS₁(T) в спектр ускорения сильного землетрясения FS₂(T) с магнитудой М₂_>М₁, в предположении что остальные параметры не меняются. Прогнозируемый спектр вычисляется по следующей формуле

FS₂(T)=П(M₁,M₂,T) FS₁(T) . (3)

После определения амплитудного спектра FS₂(T), временная функция ускорения восстанавливается по методике работы [3].

2.Результаты моделирования акселерограмм Приведем результаты моделирования искусственных акселерограмм для двух регионов Армении: Ванадзор и Гюмри. В качестве исходных данных выбираем горизонтальные составляющие ускорений двух слабых землетрясений зарегистрированных в этих регионах. Основные параметры землетрясений приведены в таблице.

Параметры исходных землетрясений

Таблица

П/Р	Дата			Н (км)	R (км)	М
Гюмри	09.06.96	40⁰49^'	43⁰34^'	10	25.9	3.9
Ванадзор	25.10.98	40⁰45^'	44⁰32^'	5	15	3.6

В обоих случаях записи получены на грунтах II категории по классификации СНРА II-2.02-94. На рис. 2 и 3 показаны исходные акселерограммы и соответствующие амплитудные спектры Фурье. С помощью выражения (3) преобразуем исходные спектры с требуемой магнитудой. В качестве требуемого значения магнитуды сильного землетрясения возьмем M₂=6.9, что соответствует магнитуде Спитакского землетрясения 7 декабря 1988 года. Вычисленные спектры и моделированные на их основе акселерограммы приведены

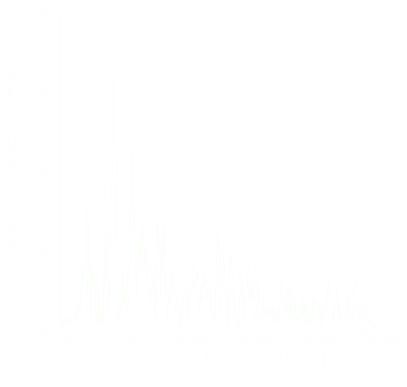
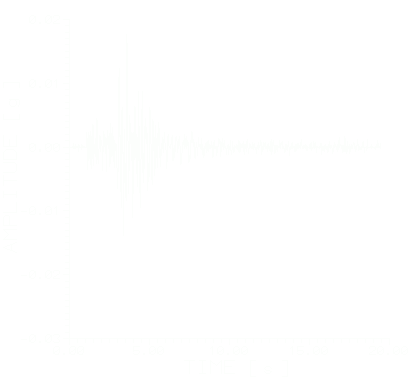
Рис.2.Акселерограмма и амплитудный спектр Фурье исходного землетрясения (Ванадзор. 25.10.98. =40⁰45^’, =44⁰32^’, M=3.6, H=5км, R=15км).

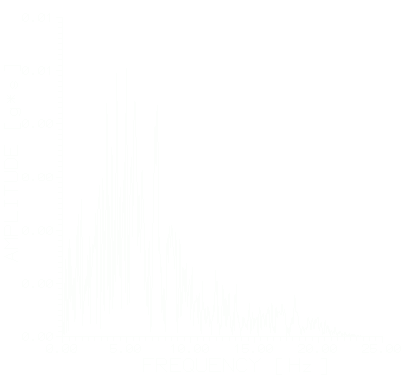
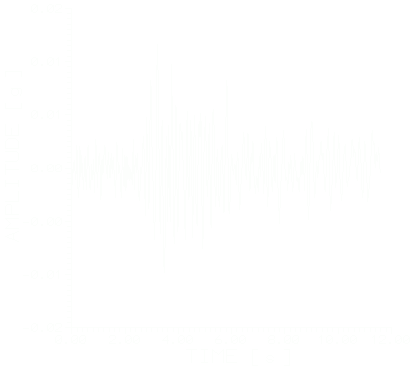
Рис.3. Акселерограмма и амплитудный спектр Фурье исходного землетрясения (Гюмри.09.06.96. =40⁰49^’, =43⁰34^’, M=3.9, H=10км, R=25.9км).

на рис.4 и 5. Сравнение исходных амплитудных спектров Фурье со спектрами преобразованных землетрясений показывает, что в исходных спектрах преобладают частоты 4Гц и больше, а в спектрах моделированных акселерограмм возрастает доля низкочастотных гармоник в диапазоне 1.6-2.4 Гц и меньше, что вполне закономерно для сильных землетрясений. Известно, что по сравнению с Ванадзором, грунты Гюмри характеризуются более низкочастотным спектром и малым затуханием [4,5]. Сравнивания рис. 4 и 5, видим, что эта закономерность соблюдается для моделированных акселерограмм и их амплитудных спектров Фурье. Спектр моделированной акселерограммы Гюмри (рис. 5) более низкочастотный, чем спектр акселерограммы Ванадзора (рис. 4). Продолжительность интенсивной части акселерограммы Гюмри составляет 20с, а продолжительность интенсивной части акселерограммы Ванадзора –12с. Таким образом, моделированные акселерограммы в основном правильно отражают реальные региональные особенности Ванадзора и Гюмри.

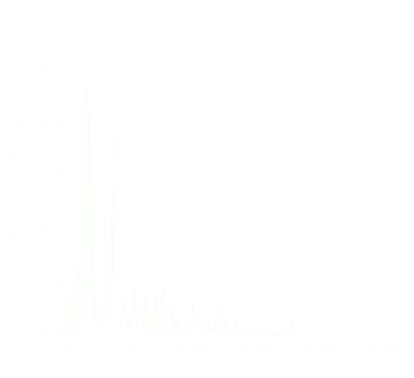
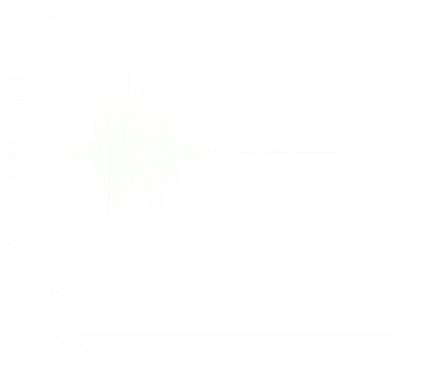
Рис.4. Моделированная акселерограмма и амплитудный спектр Фурье (Ванадзор).

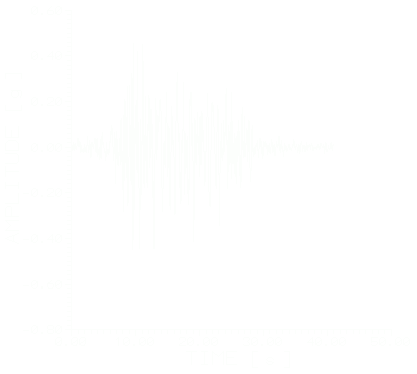
Рис.5.Моделированная акселерограмма и амплитудный спектр Фурье (Гюмри).

Сравнивались также, имеющие большое значение в теории сейсмостойкости, спектры ускорений, вычисленные по моделированным акселерограммам.

На рис. 6 показаны нормированные спектры ускорений (ξ=0.05) соответствующие акселерограмм Ванадзора и Гюмри. На этом же рисунке приведена кривая динамичности для грунтов II категории по СНРА II –2.02-94. Сравнение кривых динамичности показывает, что максимальное усиление сейсмического воздействия для Ванадзора находится в диапазоне 0.1-0.5 с, а в Гюмри –0.1-1.0с. Полученный результат согласуется данными макросейсмических и инструментальных исследований поведенными в эпицентральной зоне Спитакского землетрясения.

Рис.6. Нормированные спектры ускорений(ξ=0.05) моделированных акселерограмм: 1- Ванадзор, 2-Гюмри, 3-Кривая динамичности для грунтов II категории по СНРА II –2.02-94.

В заключение автор выражает благодарность С. М.Оганесяну за обсуждение работы.

Литература

1. Trifunac M. D. Preliminary empirical model for scaling Fourier amplitude spectra of strong ground acceleration in terms of earthquake magnitude, sourse to station distance and recording site conditions // Bull. Seism. Soc. Am. 1976. V.66.N4. P. 1343-1373.

2. Trifunac M. D., Lee V. W. Preliminary empirical model for scaling Fourier amplitude spectra of strong ground acceleration in terms of earthquake magnitude, sourse to station distance, siti intensiti and recording site conditions. Dept of Civil Eng. Rep. N CE85-03. USC. Los Angeles. 1985.

3. Trifunac M. D. A method for synthesizing realistic strong ground motion // Bull. Seism. Soc. Am. 1971. V. 61 N 6. P. 1739-1753.

4. Borcherdt R., Glassmoyer G., Andews M., Cranswick E. Effect of site conditions on ground motion and damage // Earthquake Srectra. Special supplement. Armenian earthquake reconnaissance report. Aug. 1989. P.23-42.

5. Халтурин В. И., Гедакян Э. Г., Мхитарян Л. А. и др. Усиление макросейсмического эффекта в Ленинакане // Изв. АН Арм. ССР, сер. Науки о Земле. Т. ХLIII, N 1. 1990. С. 47-50

к началу статьи